UVA10056

點我看UVA10056

題意

輸入總共有幾個玩家，勝率多少，需要求出第幾個玩家的勝率。那玩家從第一個到最後一個開始玩，如果沒有人獲勝，就到第二輪，若第二輪還沒有人獲勝，就繼續玩直到有人獲勝為止。

解題思路

先求出第一輪第i個玩家獲勝的機率，再加上第二輪第i玩家獲勝的機率...一直無限加。

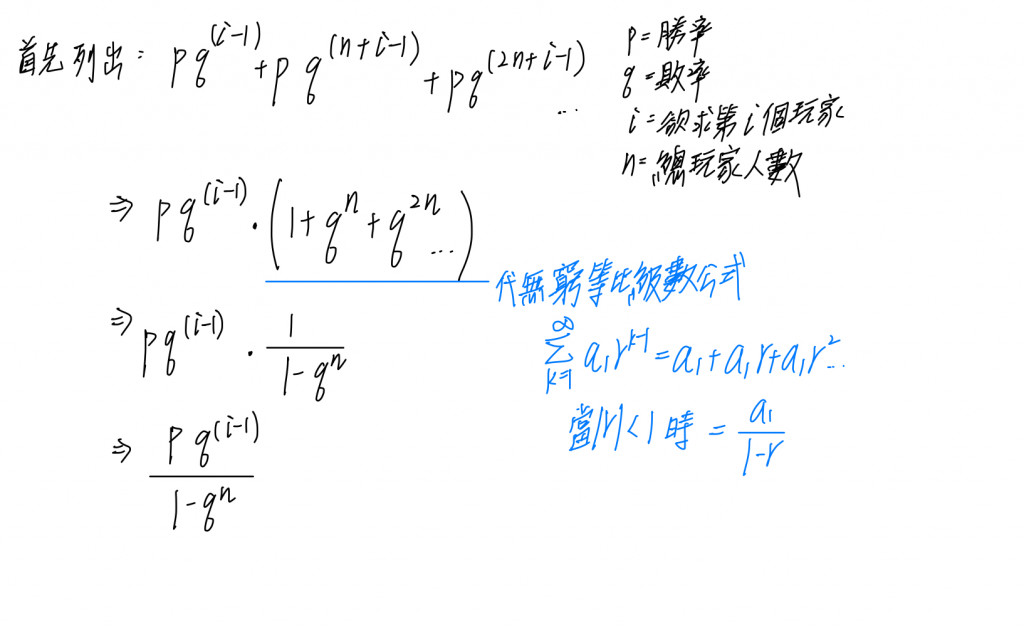
最後推導整理出的公式為(p *q^(i-1))/(1-q^n)
直接將公式帶入就可以了

注意:

1.題目要求輸出要算到小數點第四位
2.若勝率為0直接輸出0.0000即可

參考連結
http://samchien.blogspot.com/2013/04/10056-what-is-probability.html

#include<iostream>
#include<iomanip>
#include<cmath>
using namespace std;
int main(){
int s;//inputs有s組
int n;//n個玩家
float p;//單次投擲成功事件發生的概率
int i;//要算出第i個玩家獲勝的機率

cin>>s;
while(s--){
scanf("%d %f %d",&n,&p,&i);

float q=1-p;
if(p==0.0000)cout<<"0.0000"<<endl;
else
printf("%.4f\n",(p*pow(q,i-1))/(1-pow(q,n)));
}

return 0;
}

UVA10189

點我看UVA10189

題意

第一列為地圖大小，[*]表示地雷，題目需模擬遊戲中踩地雷的方式將數字填入
例如：

輸入
4 4
*...
....
.*..
....

輸出
Field #1:
100
2210
110
1110

解題思路

1.輸入的的值依序存入陣列裡，如果該值為[*]則直接先將新的陣列該位置的值放入[*]
2.開始跑回圈，若陣列中判斷到[*]時，此位置x,y座標的起始為[(x-1)][(y-1)]，依序在新的座標將周圍八個位置填入
3.計算完後輸出

#include <iostream>
#include <cstdlib>

using namespace std;

int main(){
	int n,m,count=0;
	
	while(cin>>n>>m &&n!=0)
	{
		if(count>0)cout<<endl;
		char matrix[n][m]={""}, result[n][m]={""};	
		//initinal
		for(int i=0;i<n;i++){
			for(int j=0;j<m;j++){
				cin>>matrix[i][j];
				if(matrix[i][j]=='*')result[i][j]='*';
				else result[i][j]='0';
			}
		}
		//count
		for(int i=0;i<n;i++){
			for(int j=0;j<m;j++){
				if(matrix[i][j]=='*'){
					int tmp=i-1,tmp2=j-1;
					for(int k=0;k<9;k++){
						if((tmp>=0&&tmp2>=0)&&(result[tmp][tmp2]!='*')){
							result[tmp][tmp2]=result[tmp][tmp2]+1;
							
						}
						tmp2++;
						if(tmp2>j-1+2||tmp2>=m){
							tmp2=j-1;
							if(tmp>=i-1+2)break;
							tmp++;
						}
					}
				}else continue;
					 
			}
		}
		//cout
		count++;
		cout<<"Field #"<<count<<":"<<endl;
		for(int i=0;i<n;i++){
			for(int j=0;j<m;j++){
				cout<<result[i][j];
			}
			cout<<endl;
		}
	}

}